观察经济和社会活动经常要使用许多统计指标，例如，对国家宏观经济运行状况的调查，一般要使用国内生产总值和失业率等指标、居民消费价格，进出口以及其他指标之间，各指标之间通常都有内在联系，对多个指标之间相互依赖关系及其内在统计规律性的研究，是多元统计分析中最基础的内容。
什么是多元统计分析
多元统计分析是经典统计学发展起来的一个分支，是一种多指标（也称多变量）综合分析方法，可以在多指标相互关联情况下分析其统计规律，在研究经济社会现象中具有广泛应用。
在研究经济社会现象时，会收集大量个体的多方面信息，特别是随着信息化发展，采集到个体数量和指标数量大为增加，比如网上商品交易系统采集到的信息涉及的用户数以亿计，指标数量成百上千，这些都增加了分析的难度。对这些规模宏大、复杂难辨的信息进行提炼简化，提取重要信息辅助决策，是多元统计分析的重要应用领域。同时，经济社会现象间往往存在紧密的联系，表现为统计指标之间存在相关性、因果关系等，使用多元统计分析有助于研究统计指标间的内在联系，发现经济社会现象的内在规律性。
实际观测与调查时，统计指标取值通常具有随机性，所以统计指标可表示为随机变量，则若干统计指标与若干随机变量相对应。而由若干随机变量构成的数据集合叫做随机向量，它服从某种统计分布，是建立多变量多元统计分析方法的重要依据。
多元统计分析是指研究多个变量之间的相互关系和作用的统计方法。它可以通过分析多个变量的数据，揭示它们之间的关联、差异和影响。
多元统计分析有多元方差分析，多元回归分析，主成分分析，因子分析和判别分析。这些方法有助于研究人员深入了解变量间联结关系，预测其变化，找出其隐藏结构等等。
多元统计分析的优点在于能够同时考虑多个变量之间的关系，可以提供更全面和准确的信息。它适用于各种科学研究领域，如社会科学、医学、生物学等。今天我们就来了解一下多元统计分析的几个常用方法吧：
多元统计分析法的分类
多元统计分析方法，按其分析的特点，大体可分为两大类:
一是描述性方法，主要从原始数据中提取重要信息，对系统主要特征进行研究，包括主成分分析、因子分析、聚类分析、对应分析等。
二是解析性方法，主要是研究变量间相关关系、因果关系等，通过建立模型对变量间的关系认识定量化，包括多元回归分析、判别分析、典型相关分析等。
描述性方法
1. 主成分分析
在对多指标（变量）的研究中，指标之间具有一定的相关性，造成了信息冗余，给分析带来了困难。为了达到简化指标的目的，主成分分析采用了将多个已有变量进行线性转换的方法，将它们组合为几个新的、彼此之间没有相关性的综合变量，从而最大限度地提取了原始变量的信息。例如在对地区发展的综合评价中，通常选择经济增长，科技创新，人民生活和生态环境几个指标，这几个指标通常具有相关性，利用主成分分析的方法，把这些指标归结为1~2个综合指标，有利于减少综合评价的困难。
2. 因子分析
因子分析是主成分分析的推广，将具有复杂关系的多变量转化为数量较少的几个综合变量，从而用有限个不可观测的隐变量来解释原始变量间相关关系。比如，在研究人体交感神经和副交感神经对人体的影响时，通常采集收缩压、舒张压、心跳间隔、呼吸间隔、舌下温度 5 个指标，通过因子分析可以将这 5 个指标综合为两个隐变量指标，从而反映交感神经和副交感神经的影响，找到其与原始 5 个指标的联系。
3. 聚类分析
聚类分析是将具有相似特征的个体归为一类，从而使同类的个体相似性较高， 而不同类的个体之间差异较大。衡量个体之间相似性采用“距离”测度和相似系数， 常用的“距离”测度有明式距离、马氏距离、兰氏距离，常用的相似系数有夹角余弦、相关系数。聚类分析中常用的方法有系统聚类、动态聚类等。比如，对全国省区市经济类型进行分类时，一般会选取一些的经济指标，然后利用这些经济指标计算地区与地区之间的“距离”，将“距离”近的地区归为一类，将“距离” 远的地区归为不同类别，从而形成不同地区经济发展水平类别，深化对地区经济的认识。
解析性方法
1. 多元回归分析
多元回归分析就是研究某一因变量和若干解释变量的相互依存关系、揭示因变量和被解释变量的数量关系、并以此来估算或预测因变量。例如在对经济增长的长期趋势进行预测的时候，一般都是以国内生产总值为因变量，以资本存量，就业人数，人力资本存量和制度变量为自变量，运用多元回归方法构建了经济增长与其相关因素之间的定量模型并运用所得模型关系预测了经济增长的未来趋势。
2. 判别分析
判别分析是判别观察个体所属类别的一种统计分析方法，它是在已知观察个体分为若干个类别的条件下，通过建立判别规则，对观察个体进行判别分类。它与聚类分析最大不同是，聚类分析事先不知道观察个体有多少个类别，而判别分析事先已知观察个体的类别个数。常用的判别分析法有距离判别法、费舍尔判别法、贝叶斯判别法等。比如，世界银行将全球国家划分为高收入国家、中高收入国家、中低收入国家、低收入国家四种类型，当判断一个国家属于哪种类型时， 可以使用判别分析方法建立规则进行判别。
示例
为了分析我国经济增长驱动因素及效应，在柯布—道格拉斯生产函数基础上构建了多元回归测算模型:
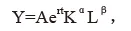
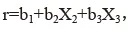
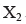
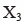
其中，Y、K、L 分别为总产出、资本投入、劳动投入，r 为技术进步率、t 为时间，α、β 分别为资本投入、劳动投入的弹性。假定技术进步率不为常数，将其设定为，其中分别和第二产业和第三产业就业人员比例，带入上述生产函数，并假定规模报酬不变，即 α+β=1，可以得到：
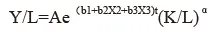
记 Y/L=y，K/L=k，取对数后对公式两边进行变换，可以得到：考虑到变量非平稳性，对上式两边进行差分后回归测算，使用 1978—2013 年我国的国内生产总值、资本存量和就业人数等数据得到：
多元回归检验所显示的回归结果良好，以上模型可以满足经济产出，资本投入和劳动投入三者关系分析的要求。由回归结果可知，增加人均资本存量对人均经济产出有促进作用。
